Introduction

In this post, we take a look at what insurance companies and pension plans are, what risks they face, and how they are hedged. We also compute and visualize, in Python, some survival probabilities and expected payouts for the insurance companies using a real UK mortality table from 2020.

Insurance Companies

First, let’s define some terms. An insurance company offers protection against unfavourable events. The contract defining the terms of the protection is called a policy. The individual who buys the policy from the insurance company is called a policyholder.

Usually, the policyholder makes regular (e.g. monthly) payments called premiums to the insurance company. These payments are made until the unfavourable event occurs. For example, in the case of life insurance, the policyholder makes premium payments until they die, when they (or better said, their family) receive a large lump sum.

The three main categories of insurance are:

• life insurance

• property and casualty insurance

• health insurance

Each of these will be discussed in further sections.

Mortality tables

Mortality tables are the most important tool insurance companies use to determine what the probabilities of survival are.

Here’s a real life UK mortality table for males from 2020.

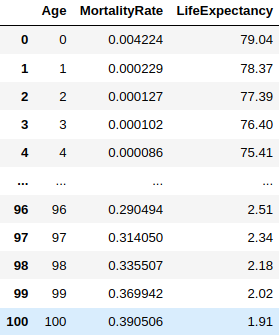
There are only three columns, but that should be enough to derive quite a lot of insight about what the premiums should be and what the survival probabilities are. For each age, we have the mortality rate, which is the probability of death within the next year. The survival probability is 1 - mortality rate. The mortality rate is relatively high for newborns as they are at a higher risk of complications. Once newborns survive their first year, the mortality rate decreases progressively. Each year survived increases the odds of surviving another year, up until some point, after which it starts to decrease again.

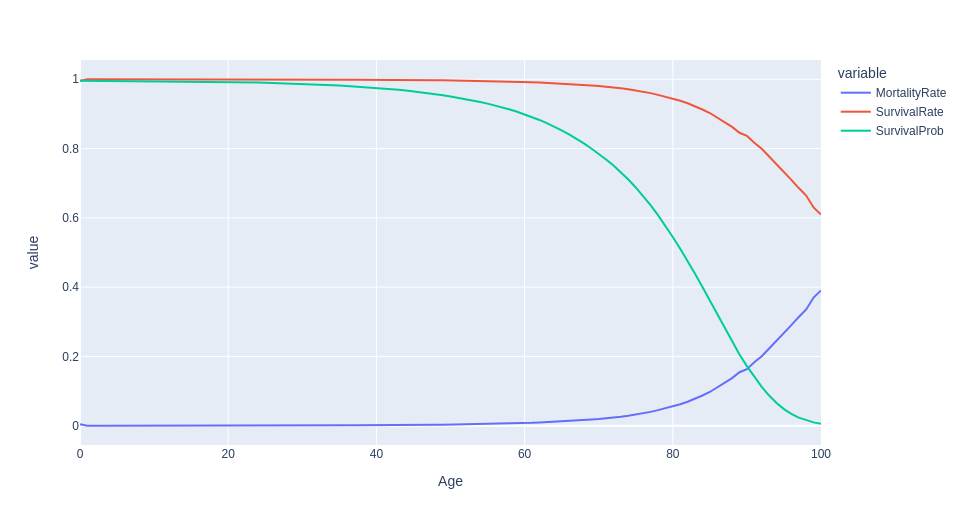
Consequently, the life expectancy of a newborn male is 79. However, as more years pass, the expected age of death is pushed further and further away, such that a male who reaches 79 is expected to live for another 8.87 years! At age 99, a male is expected to live for another two more years! Pretty good I would say.

Here’s the code for computing the survival rate and probability.

def add_survival_probability(df: pd.DataFrame) -> pd.DataFrame:
    df_return = df.copy()
    df_return['SurvivalRate'] = 1 - df['MortalityRate']
    df_return['SurvivalProb'] = np.cumprod(df_return['SurvivalRate'])
    return df_return

df_survival = add_survival_probability(df)
df_survival.plot(x='Age', y=['MortalityRate', 'SurvivalRate', 'SurvivalProb'])

Now, assume we are an insurance company and we want to sell a policy to a 30-year old male. Therefore, we need to compute our expected payouts based on his survival probability conditional on him being 30-years old.

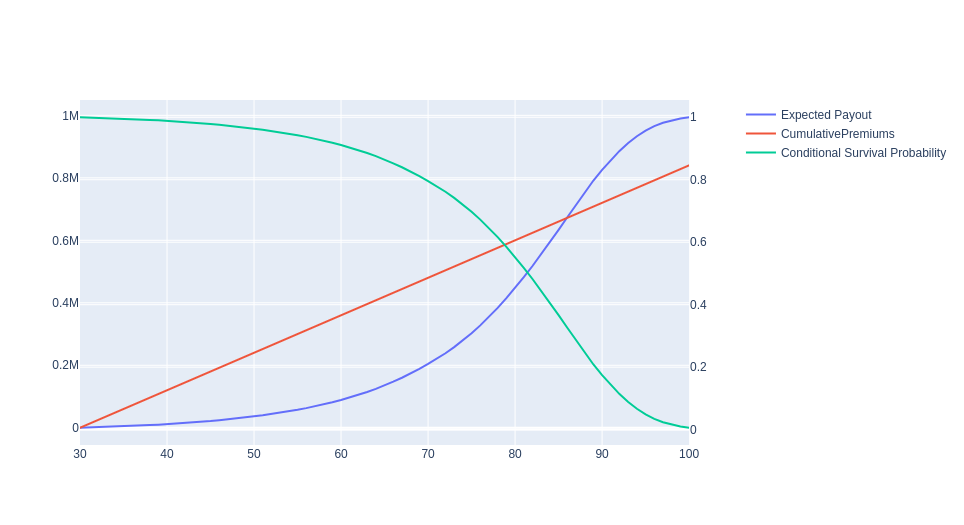
As we can see from the graph, for a $1 million face value policy owned by a 30-year old male paying $1’000 per month, the insurance company should expect, on average, to be in a deficit from the moment he reaches 85 onwards. This is plenty of time for the insurance company to increase the value of the premiums by investing them in safe assets.

Again, here’s the code:

def compute_expected_payouts(df, face_value: float, policyholder_age: int, premium: float):
    df_where = df.query(f"Age >= {policyholder_age}")
    df_result = df_where.copy()
    base_survival_prob = df_where.iloc[0]['SurvivalProb']
    print(f'{base_survival_prob=}')
    # Conditional on the policyholder reaching the input age, what is the survival probability of them
    # reaching each age.
    df_result['ConditionalSurvivalProb'] = df_result['SurvivalProb'] / base_survival_prob
    df_result['ExpectedPayout'] = face_value * (1 - df_result['ConditionalSurvivalProb'])
    df_result['CumulativePremiums'] = (df_result.index - policyholder_age) * premium
    return df_result
    
df_expected_payout = compute_expected_payouts(
    df=df_survival,
    face_value=1_000_000, 
    policyholder_age=30, 
    premium=12_000
)

Mortality risk vs Longevity risk

Mortality risk is the risk of policyholders dying earlier than what the initial average life expectancy predicted at the time the contract was initiated.

The reverse of the medal is longevity risk, which is the risk of policyholder living longer than expected.

Different companies have different risks. Whole life insurance companies face mortality risk, i.e. the risk that its policyholder die sooner than expected, paying fewer premiums. On the other hand, insurance companies offering annuity contracts suffer from longevity risk - the more their policyholders live, the more they have to pay.

Clearly, these risks are the opposite, which is why insurance companies with business both in whole life insurance and annuities can offset these risks to some degree. The rest of the risks can be hedged using forwards on the mortality rate.

Defined Benefit Plans vs Defined Contribution Plans

There are two types of pension plan.

Defined benefit plans are plans in which the employer pools money from its employees and invests it. There are usually guarantees in terms of the amount that will be received by the employee. This means that the company has to step in if the funds it invested didn’t grow to cover its liabilities. Obviously, this is very risky for the company and the reason why defined benefit plans are not offered anymore these days.

The more common plans nowadays are defined contribution plans, in which the employer invests the pension on the behalf of the employee. This means that the employer has no liability in the future.

Life insurance policies

There are many types of life insurance policies, with different characteristics and purposes.

• Whole life insurance. This was discussed above with example expected payouts.

• Term life insurance. Similar to whole life insurance, but only valid for a certain number of years.

• Group life insurance. Purchased by companies for their employees.

• Endowment life insurance. Term life insurance where the payout is certain at the end of the maturity. Sometimes there is also a payout in case of early death, or illness.

• Annuity contracts. These are contracts in which an annuity (payment) is made after a pre-determined date - think about them like pensions, where you first make contributions (premiums), then you get a guaranteed annuity.

Property-casualty insurance

Property-casualty insurance companies are different than life insurance companies, because they don’t offer a payout on events pertaining to life, but rather to property. For example, car insurance and home insurance fall into this category.

Property-casualty insurance companies have to manage two types of risk. - risks which can be estimated fairly accurately from historical trends (e.g. the number of car accidents in a country), and where payouts are relatively uncorrelated and spread out across policyholders. - catastrophic risks, like hurricanes and earthquakes, which are rarer and cannot be predicted and where all policyholders require payouts at the same time.

While catastrophic risks are much harder to predict, they can be hedged somewhat using catastrophe bonds (CAT bonds), which offer regular principal payments to their holders and its face value at the maturity (like normal bonds), but in case of a catastrophe, the face value of the bond may not be returned by the issuer of the bond.

Health insurance

Health insurance is a form of insurance which offers a payout in case of illnesses. The most important distinction from the other types of insurance is that health insurance premiums can only increase if healthcare costs increase. The insurance company cannot raise your premiums after finding out you have a disease or illness, like in the case of car insurance companies, which are allowed to increase your premiums if you drive more aggressively (e.g. as measured by the number of speed tickets or accidents you have been involved in).

Moral hazard and Adverse selection

In the previous section, we talked about how car insurance companies can charge higher premiums for drivers who, for example, have more speed tickets, but not for people just diagnosed with an illness. Why is that?

The reason for this are two concepts called moral hazard and adverse selection. Moral hazard refers to situations in which insured parties behave in a more risky manner, because they know they will receive a payout if things go awry. For instance, if you have insurance on your laptop, you may not be as careful with your cup of coffee around it.

Adverse selection refers to insurance policies which attract the riskiest policyholders. For instance, a policy which does not discriminate among car drivers will likely attract the worst drivers, as they will pay the same premiums as everyone else, even though they drive most recklessly.

Capital Requirements

Whilst banks have the Basel Committee recommendations, insurance companies have no globally accepted capital requirements.

In the United States, each state legislates its own capital requirements for insurance companies.

In Europe, from 2016 onwards, a framework called Solvency II was implemented. It specifies two distinct capital requirements:

• solvency capital requirements (SCR) - if the capital of an insurance company falls below this level, it must develop a plan to bring it back up again.
• minimum capital requirements (MCR) - if the capital falls below this level, the firm may not take up new business, and its existing business may be transferred to other companies.

MCR is around 25% to 45% of SCR.